Note
This tutorial was generated from a Jupyter notebook that can be downloaded here.
The null space¶
A key principle in the problem of mapping the surfaces of stars and planets is the idea of a null space. The null space of a (linear) transformation is the set of input vectors that result in a zero vector as output. In the context of mapping, the null space comprises the spherical harmonics (or combinations of spherical harmonics) that do not affect the observed flux whatsoever.
A trivial example is the \(Y_{1,-1}\) spherical harmonic, which does not project into the light curve for rotations about the vertical (\(\hat{y}\)) axis:
It is clear that as this object rotates, the total flux does not change (and in fact is exactly zero). That’s because the \(Y_{1,-1}\) harmonic is perfectly symmetric under such rotations.
It might be hard to think of other harmonics that behave this way, but in fact the vast majority of spherical harmonics are usually in the null space of the light curve problem. Let’s take a deeper look at this. First, we’ll load starry and generate a high resolution map of the Earth.
[5]:
import matplotlib.pyplot as plt
import numpy as np
import starry
starry.config.lazy = False
starry.config.quiet = True
[6]:
map1 = starry.Map(30)
map1.load("earth", sigma=0.05)
map1.show(projection="rect")
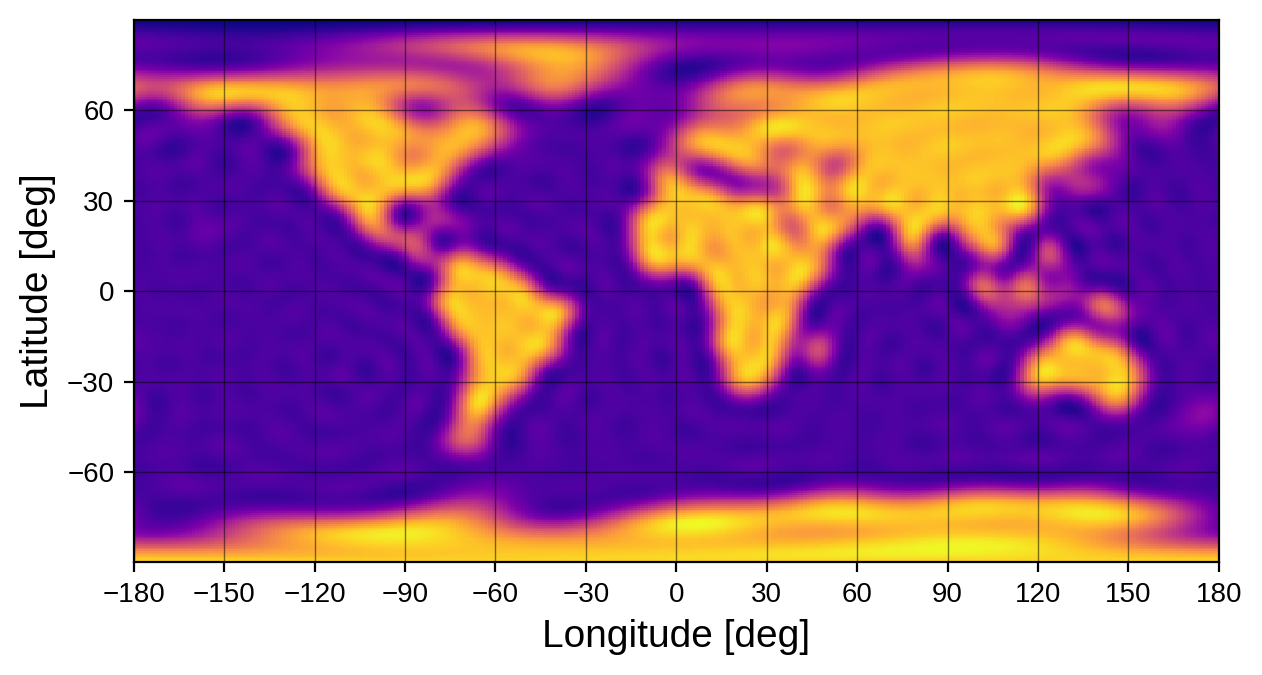
Let’s now compute the light curve of this map as we rotate it one full cycle about the \(\hat{y}\) direction:
[7]:
theta = np.linspace(0, 360, 1000)
flux1 = map1.flux(theta=theta)
plt.figure(figsize=(12, 5))
plt.plot(theta, flux1)
plt.xlabel(r"$\theta$ [degrees]", fontsize=24)
plt.ylabel("Flux [arbitrary units]", fontsize=24);
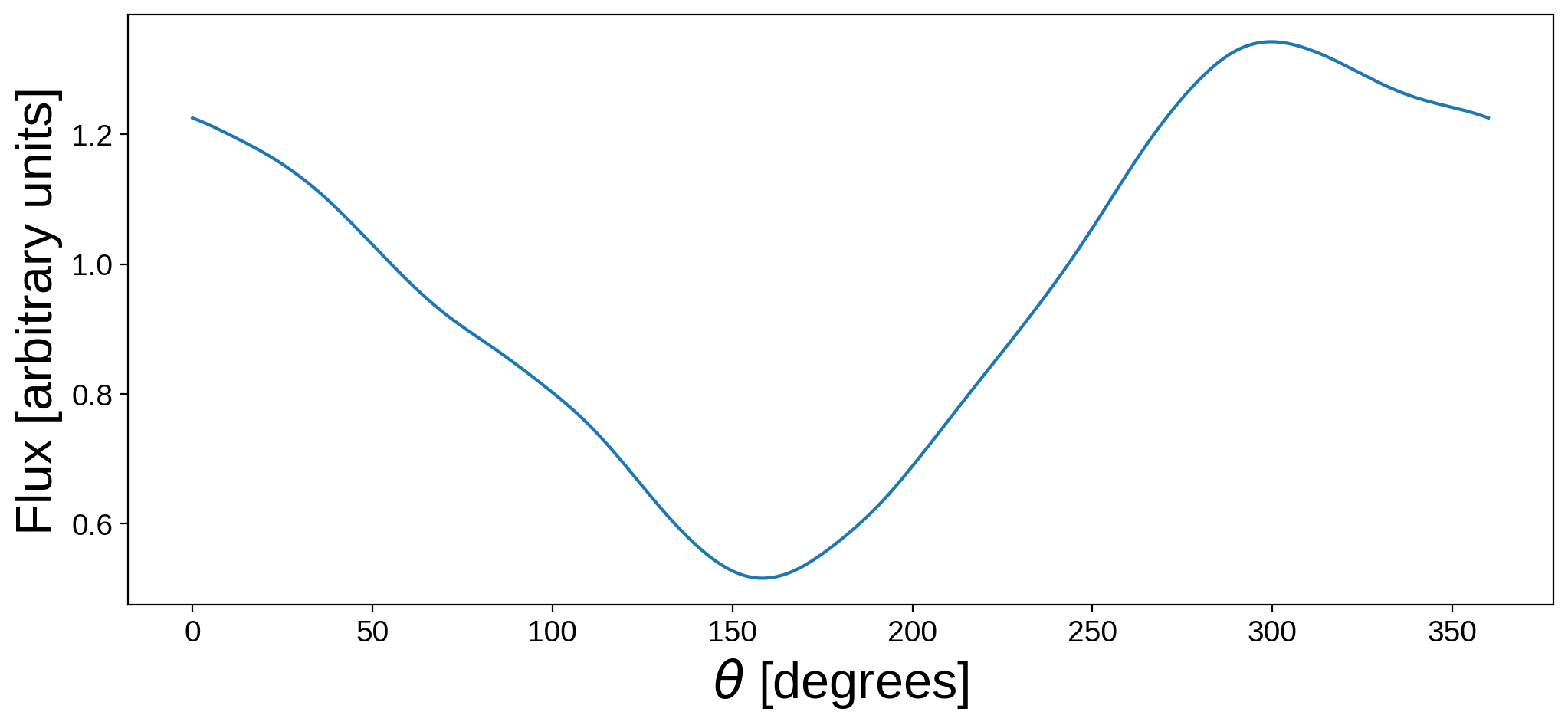
At phase 0, the prime meridian is facing the observer, and the flux drops as the Atlantic and then Pacific oceans come into view. The flux then peaks when Asia is in view, and that’s the light curve of the Earth.
Now, let’s create a new, identical map of the Earth:
[8]:
map2 = starry.Map(30)
map2.load("earth", sigma=0.05)
But this time, we’ll change all coefficients corresponding to odd degrees above 2…
[9]:
for l in range(3, map2.ydeg + 1, 2):
map2[l, :] = 1e-3 * np.random.randn(len(map2[l, :]))
… as well as all coefficients corresponding to negative values of m:
[10]:
for l in range(1, map2.ydeg + 1):
map2[l, -l:0] = 1e-3 * np.random.randn(len(map2[l, -l:0]))
Here’s what this silly map looks like:
[11]:
map2.show(projection="rect")
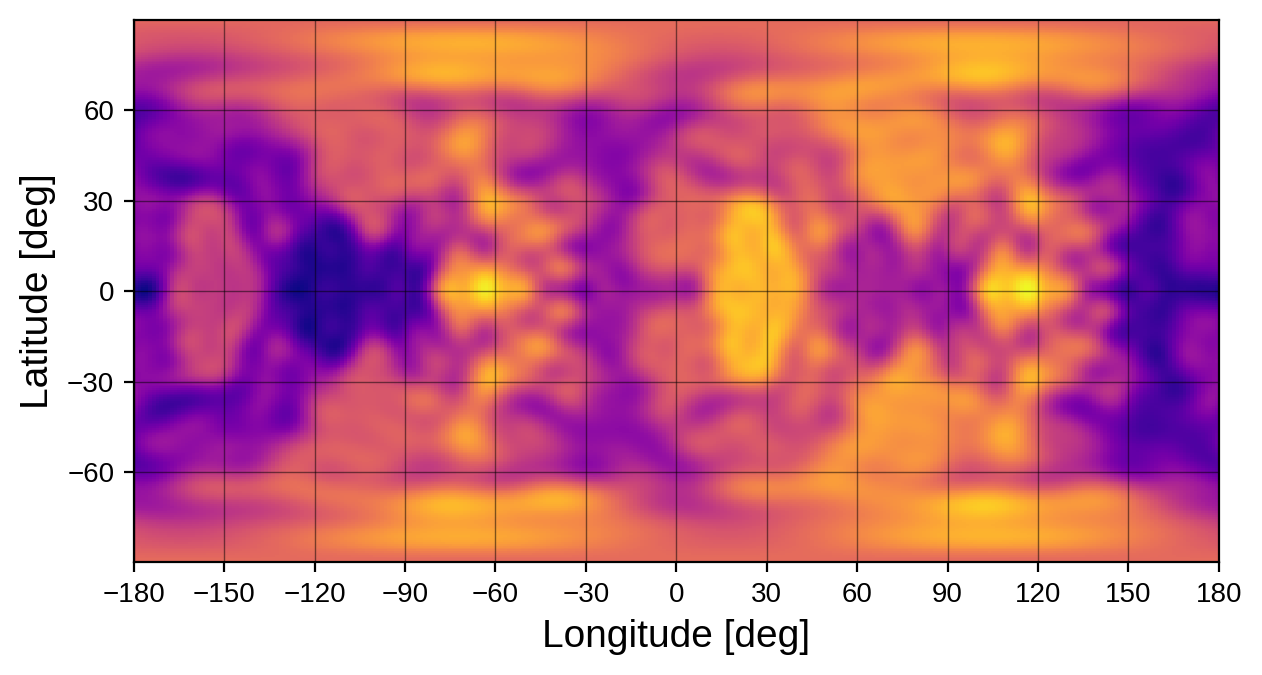
It doesn’t really look anything like the Earth (though a sharp eye might spot the outline of Africa and some other familiar features – barely). If you’re wondering why we did this, let’s plot the light curve of this new map next to the light curve of the original map of the Earth:
[12]:
flux2 = map2.flux(theta=theta)
plt.figure(figsize=(12, 5))
plt.plot(theta, flux1, label="map1")
plt.plot(theta, flux2, "--", label="map2")
plt.legend()
plt.xlabel(r"$\theta$ [degrees]", fontsize=24)
plt.ylabel("Flux [arbitrary units]", fontsize=24);
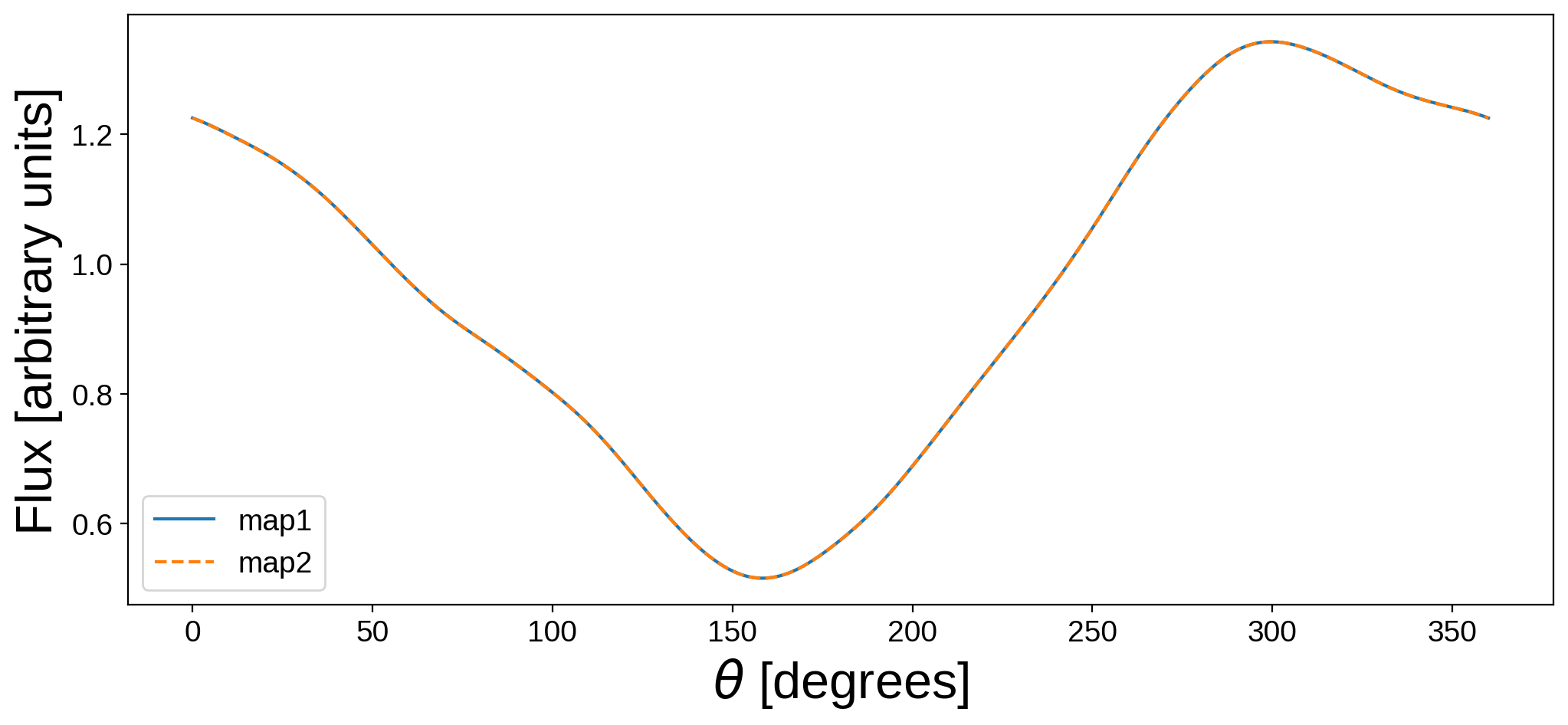
Their light curves are identical. Even though the maps look completely different, the actual differences between the two maps lie entirely in the null space (by construction). This means we have no way of distinguishing between these two maps if all we have access to is the light curve.
To drive this point home, here’s what the two maps look like side-by-side:
[13]:
map1.show(theta=np.linspace(0, 360, 50))
map2.show(theta=np.linspace(0, 360, 50))
The total amount of flux at any given time – equal to the brightness integrated over the entire disk – is the same in both cases, even though the surfaces look nothing alike.
For objects rotating along an axis perpendicular to the line of sight (as in the example above), the null space consists of all of the \(m < 0\) harmonics, as well as all of the harmonics of degree \(l = 3, 5, 7 ...\):
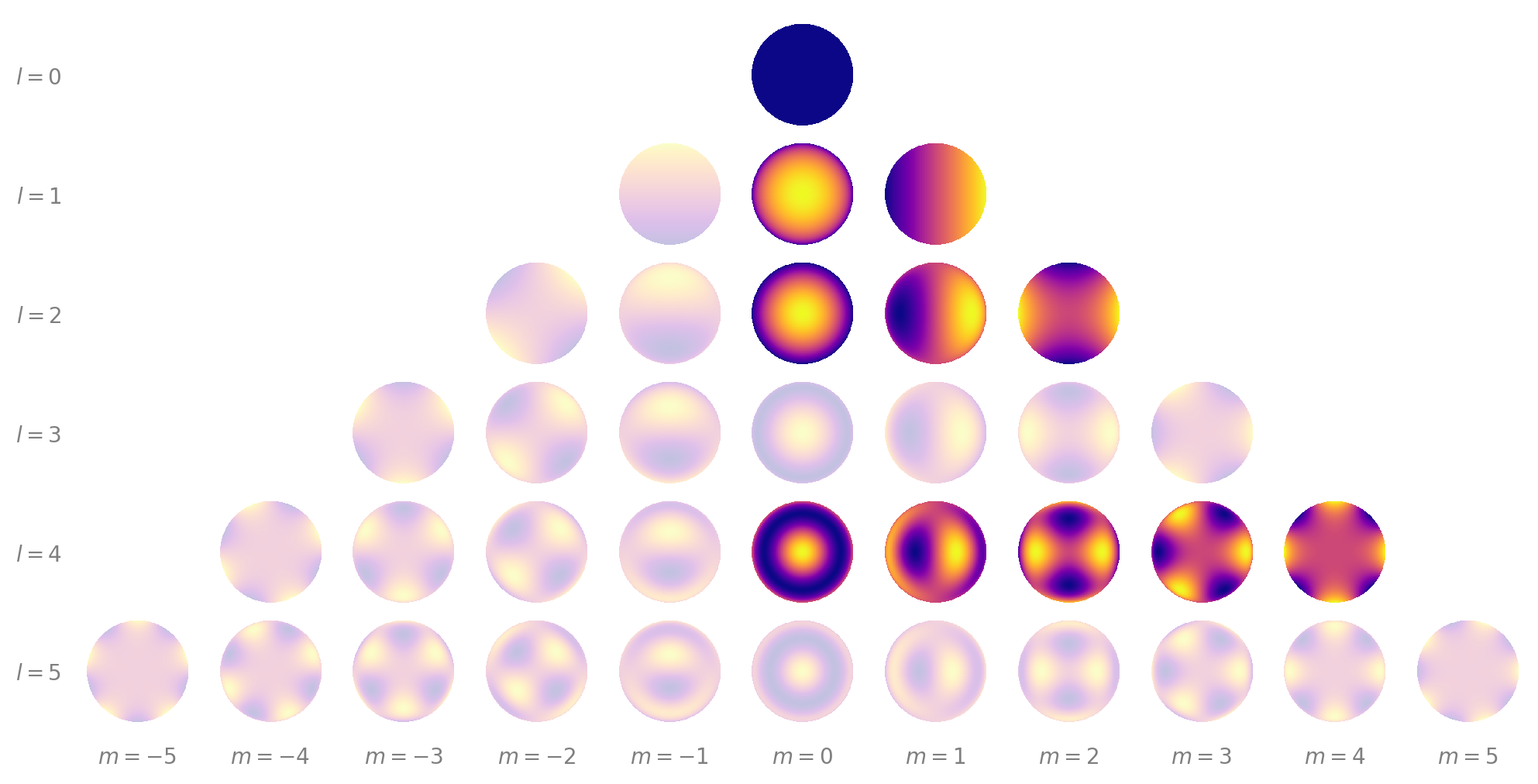
The null space for this problem is indicated by the translucent harmonics above. (Note that in general certain linear combinations of the remaining harmonics are also in the null space, so the problem is actually worse than in the example above).
The size of the null space¶
Because the light curve model in starry is linear, it’s actually easy to compute the size of the null space for a given problem. Consider how the flux \(\mathbf{f}\) is computed in starry:
where \(\mathbf{A}\) is the design matrix (which you can obtain from map.design_matrix()) and \(\mathbf{x}\) is just the (amplitude-weighted) spherical harmonic coefficient vector. When solving this system for \(\mathbf{x}\), the matrix we end up needing to invert looks like
where \(\Sigma\) is the data covariance matrix. The object \(\mathbf{I}\) is the Fisher information matrix and quantifies the maximum amount of information we can learn given our observations \(\mathbf{f}\). While there’s a lot we can do with \(\mathbf{I}\), the most important thing in our case is the size of the null space, which is equal to the number of rows (or columns) minus the rank of this matrix.
There’s lots of ways to think about why this is the case. Note that \(\mathbf{I}\) is invertible if (and only if) it is full rank, meaning the null space is zero. That’s the condition for a well-posed problem, in which we can learn everything there is to know about \(\mathbf{x}\) from our observations \(\mathbf{f}\). In nearly all cases in the mapping problem, \(\mathbf{I}\) is not full rank, meaning it has linearly dependent rows or columns. For each such column, that’s one fewer term (or combination of terms) we are able to constrain in \(\mathbf{x}\). In other words, the size of the null space is equal to the number of linearly dependent rows/columns in \(\mathbf{I}\).
Note, importantly, that in the limit that our measurements are uncorrelated, the rank of \(\mathbf{I}\) is equal to the rank of \(\mathbf{A}^\top \mathbf{A}\) (i.e., independent of the uncertainties). Note also that this quantity does not depend on either \(\mathbf{f}\) or \(\mathbf{x}\) – just the design matrix!
Let’s take a look at the size of the null space in the problem above. We’ll use numpy.linalg.matrix_rank to compute the matrix rank.
[15]:
def compute_info(A):
"""Compute some information about the null space of the design matrix A."""
# Get the Fisher information & compute its rank
I = A.T.dot(A)
R = np.linalg.matrix_rank(I)
# Number of coefficientss
C = I.shape[0]
# Size of null space
N = C - R
# Fractional size of null space
F = N / C
# Show it graphically
fig, ax = plt.subplots(figsize=(6, 0.3))
ax.set_xlim(0, 1)
ax.axis("off")
ax.axvspan(0, 1 - F, color="C0")
ax.axvspan(1 - F, 1, color="red")
ax.annotate(
"{}/{}".format(R, C),
color="C0",
fontsize=10,
xy=(-0.025, 0.5),
xycoords="axes fraction",
va="center",
ha="right",
)
ax.annotate(
"{:.0f}%".format(100 * F),
color="w",
fontsize=10,
xy=(1 - 0.5 * F, 0.5),
xycoords="axes fraction",
va="center",
ha="right",
)
[16]:
A = map1.design_matrix(theta=theta)
compute_info(A)

The red bit represents the null space, while the blue bit represents the terms we can constrain from the data (the “image” of the linear transformation). Our problem has 961 free coefficients, but the rank of the Fisher matrix is only 33. That means that 928 of the coefficients (or, more precisely, 928 linear combinations of coefficients) lie in the null space. In other words, 97 percent of the information about the map cannot be probed from the light curve in this case.
Yep. 97 percent.
So, how can we possibly map other stars and planets?¶
There are several ways to get around the information issue, and they all involve finding ways to break degeneracies. Below is a non-exhaustive list of ideas.
Lower degree maps¶
The size of the null space increases pretty steeply with the degree of the map. That’s because we can typically only constrain up to two terms per spherical harmonic degree from a light curve (a cosine term and a sine term); but the number of terms increases quadratically with the degree of the map. Let’s look at the size of the null space for a 5th degree map (instead of 30th):
[17]:
map = starry.Map(5)
A = map.design_matrix(theta=theta)
compute_info(A)

It’s better – now the size of the null space is only 81%. The high order terms are usually the hardest ones to constrain!
Inclined maps¶
There’s a perfect degeneracy for maps seen at an inclination of 90 degrees, since there’s no way to differentiate between the northern and southern hemispheres of the map – they contribute equally to the light curve. As long as there’s a little inclination, that degeneracy is broken. Consider a map seen at 60 degrees inclination:
[18]:
map = starry.Map(5)
map.inc = 60
A = map.design_matrix(theta=theta)
compute_info(A)

Again, we’ve chipped away at the null space some! But note: this applies when we know the inclination exactly. If we need to solve for it (or marginalize over it), we’ll obviously be dealing with extra uncertainty.
Limb darkening¶
The presence of limb darkening causes different parts of the map to be weighted differently at different phases. This breaks further symmetries in the problem:
[19]:
map = starry.Map(5, 1)
map.inc = 60
map[1] = 0.5
A = map.design_matrix(theta=theta)
compute_info(A)

Note, again, that above we assume we know the limb darkening law exactly, which is never the case in practice!
Transits and occultations¶
Transits or occultations break many symmetries. Let’s transit a small body across our map as it rotates, and look at the null space of the problem. We’ll have the body transit twice, occulting a different portion of the map each time (since it’s rotating).
[20]:
map = starry.Map(5, 1)
map.inc = 60
map[1] = 0.5
xo = 1.5 * np.sin(2 * np.pi * np.linspace(0, 2, len(theta)) + 0.5 * np.pi)
yo = 0.3
zo = 1.5 * np.cos(2 * np.pi * np.linspace(0, 2, len(theta)) + 0.5 * np.pi)
ro = 0.1
A = map.design_matrix(theta=theta, xo=xo, yo=yo, zo=zo, ro=ro)
compute_info(A)

The presence of an occultor has made a huge difference: the size of the null space is now nearly zero! Here’s what a light curve might look like for this situation:
[21]:
map.load("earth")
flux0 = A.dot(map.y)
sigma = 1e-3
flux = flux0 + sigma * np.random.randn(len(flux0))
plt.plot(theta, flux)
plt.xlabel("angular phase [deg]")
plt.ylabel("flux [normalized]");
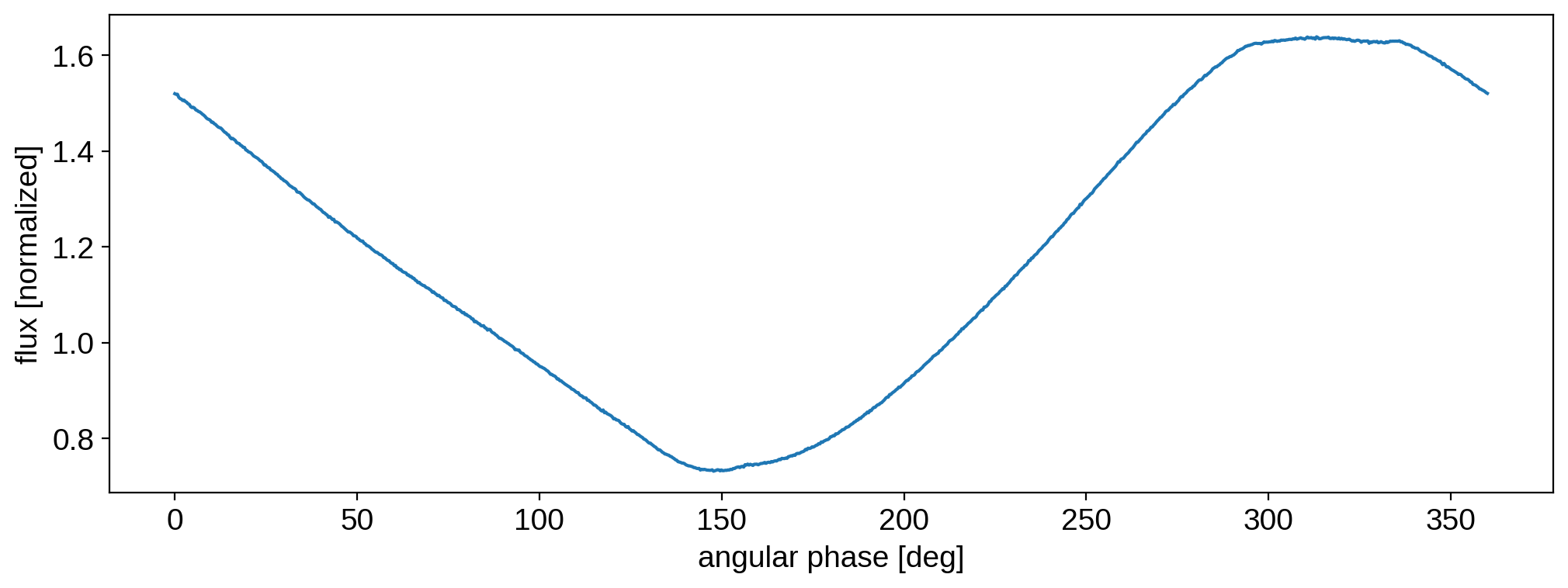
You can see the small transits at angular phases of 150 and 300 degrees. Given this light curve, let’s add a Gaussian prior on the coefficients and linearly solve for the map:
[22]:
map.set_data(flux, C=sigma ** 2)
map.set_prior(L=1e-4)
map.solve(design_matrix=A)
map.show(projection="rect")
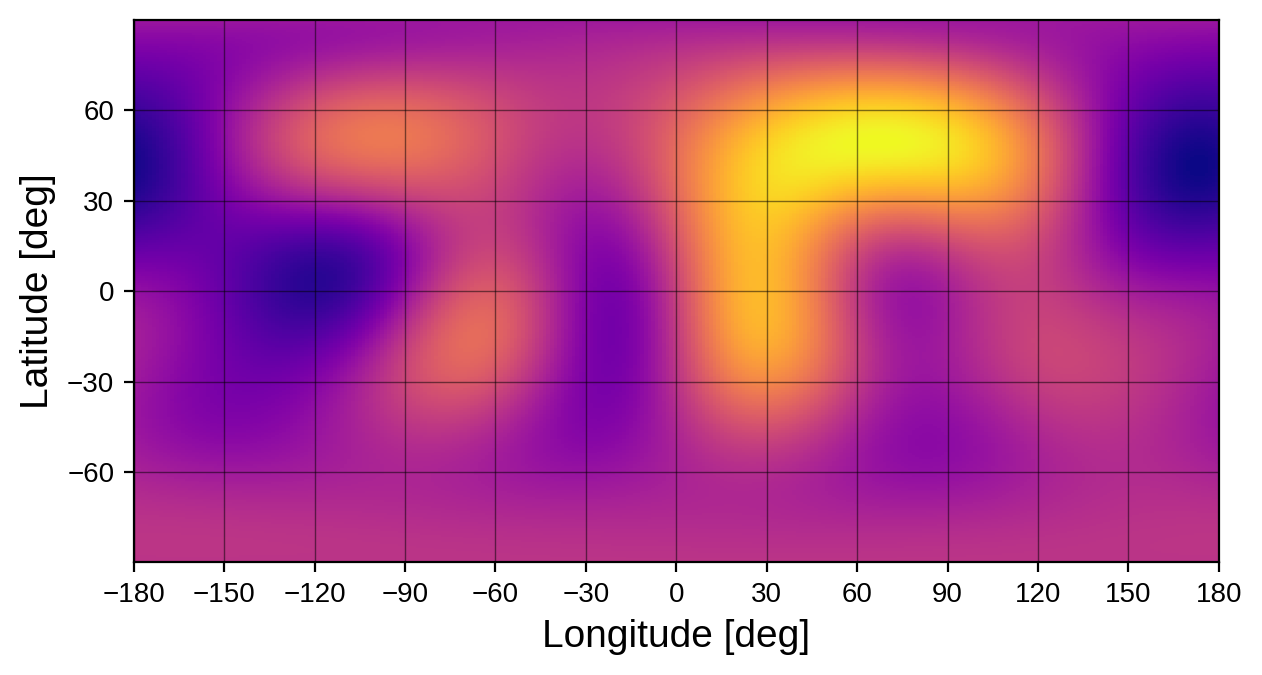
Here’s the true map for reference:
[23]:
map.load("earth")
map.show(projection="rect")

As expected, we did quite well! Although it’s blurry, we can pick out the major continents and oceans. The punchline: transits and occultations are great ways to break degeneracies. Stars transited by (multiple) planets or stars in eclipsing binary systems are therefore excellent targets for mapping.
Note
The example above is super idealized. The flux error was extremely small, we knew the inclination, limb darkening coefficients, and occultor parameters exactly, and we had transits across different portions of the surface. In most cases, things will not be this ideal, and the null space will be larger and/or the recovered maps will have much larger uncertainty.
Reflected light¶
The last thing we’ll touch on is phase curves in reflected light. Consider the idealized case of an inclined planet illluminated by a star with a rotational period that’s different from its orbital period:
[24]:
map = starry.Map(5, reflected=True)
map.inc = 60
xs = np.sin(2 * np.pi * np.linspace(0, 1.33, len(theta)))
ys = np.sin(2 * np.pi * np.linspace(0, 1.33, len(theta)))
zs = np.cos(2 * np.pi * np.linspace(0, 1.33, len(theta)))
A = map.design_matrix(theta=theta, xs=xs, ys=ys, zs=zs)
compute_info(A)

There is no null space! This example is highly contrived (the null space pops back up as soon as you increase the degree of the map, for instance) but it shows how powerful reflected light can be. The reason is that the day/night terminator breaks most of the symmetries in the problem, especially if it precesses relative to the rotational axis (as it does for an inclined planet).