Note
This tutorial was generated from a Jupyter notebook that can be downloaded here.
Multi-wavelength maps¶
Nearly all of the computational overhead in starry comes from computing rotation matrices and integrals of the spherical harmonics, which makes it really fast to compute light curves at different wavelengths if we simply recycle the results of all of these operations.
By “multi-wavelength” we mean a map whose spherical harmonic coefficients are a function of wavelength. Specifically, instead of setting the coefficient at \(l, m\) to a scalar value, we can set it to a vector, where each element corresponds to the coefficient in a particular wavelength bin. Let’s look at some examples.
[3]:
import numpy as np
import matplotlib.pyplot as plt
import starry
starry.config.lazy = False
starry.config.quiet = True
The basics¶
Let’s instantiate a simple map with nw=3 wavelength bins:
[4]:
map = starry.Map(ydeg=2, nw=3)
Normally, the y attribute of a map is its spherical harmonic coefficient vector, but in this case it is a matrix with \(N_y = (l + 1)^2 = 9\) rows and \(n_w = 3\) columns:
[5]:
map.y
[5]:
array([[1., 1., 1.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
Each row corresponds to a given spherical harmonic, and each column to a given wavelength bin. Let’s set the \(Y_{1,0}\) coefficient:
[6]:
map[1, 0, :] = [0.3, 0.4, 0.5]
Here’s our new map vector:
[7]:
map.y
[7]:
array([[1. , 1. , 1. ],
[0. , 0. , 0. ],
[0.3, 0.4, 0.5],
[0. , 0. , 0. ],
[0. , 0. , 0. ],
[0. , 0. , 0. ],
[0. , 0. , 0. ],
[0. , 0. , 0. ],
[0. , 0. , 0. ]])
To visualize the map, we can call map.show() as usual, but now we actually get an animation showing us what the map looks like at each wavelength.
[8]:
map.show(interval=500)
Let’s set a few more coefficients:
[9]:
map[1, -1, :] = [0, 0.1, -0.1]
map[2, -1, :] = [-0.1, -0.2, -0.1]
map[2, 2, :] = [0.3, 0.2, 0.1]
[10]:
map.show(interval=500)
Phase curves¶
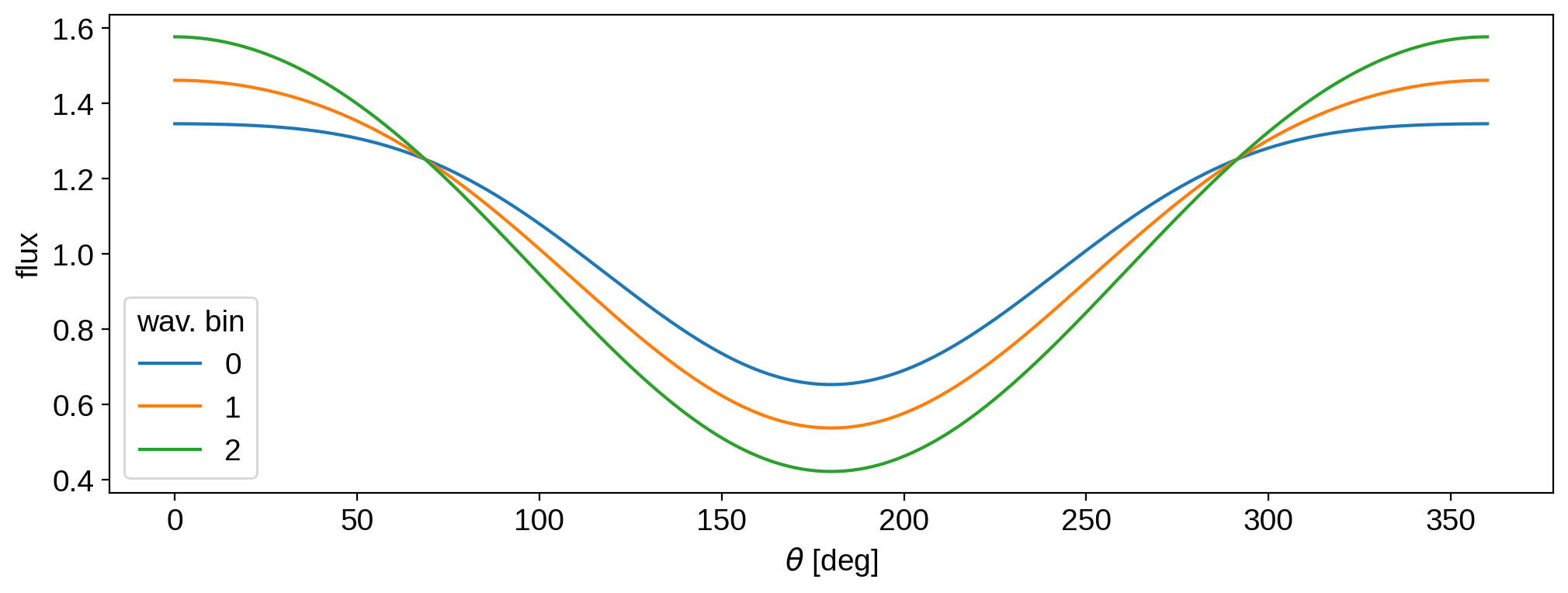
OK, our map now has some interesting wavelength-dependent features. Let’s compute some light curves! First, a simple phase curve:
[11]:
theta = np.linspace(0, 360, 1000)
phase_curves = map.flux(theta=theta)
for i, phase_curve in enumerate(phase_curves.T):
plt.plot(theta, phase_curve, label=i)
plt.xlabel(r"$\theta$ [deg]")
plt.legend(title="wav. bin")
plt.ylabel("flux");
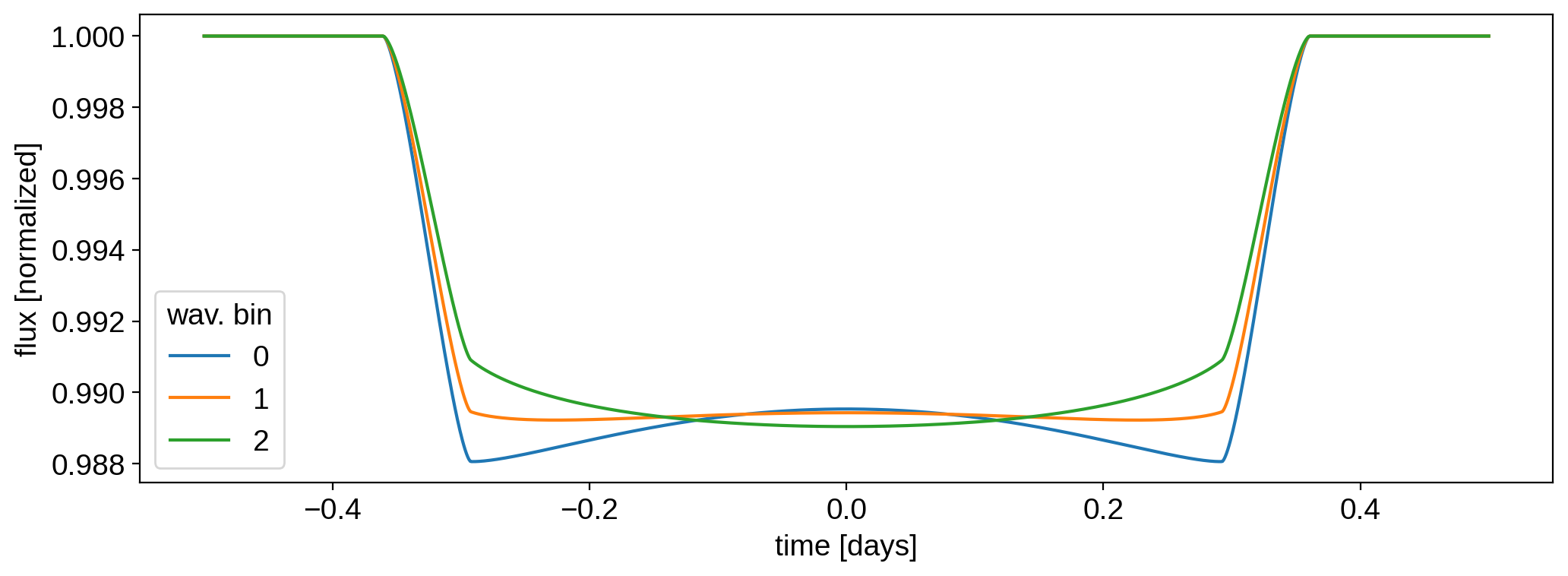
Occultations¶
We can also compute an occultation light curve:
[12]:
t = np.linspace(-0.5, 0.5, 1000)
xo = np.linspace(-1.5, 1.5, 1000)
light_curves = map.flux(xo=xo, yo=0.2, ro=0.1)
for i, light_curve in enumerate(light_curves.T):
plt.plot(t, light_curve / light_curve[0], label=i)
plt.xlabel(r"time [days]")
plt.legend(title="wav. bin")
plt.ylabel("flux [normalized]");
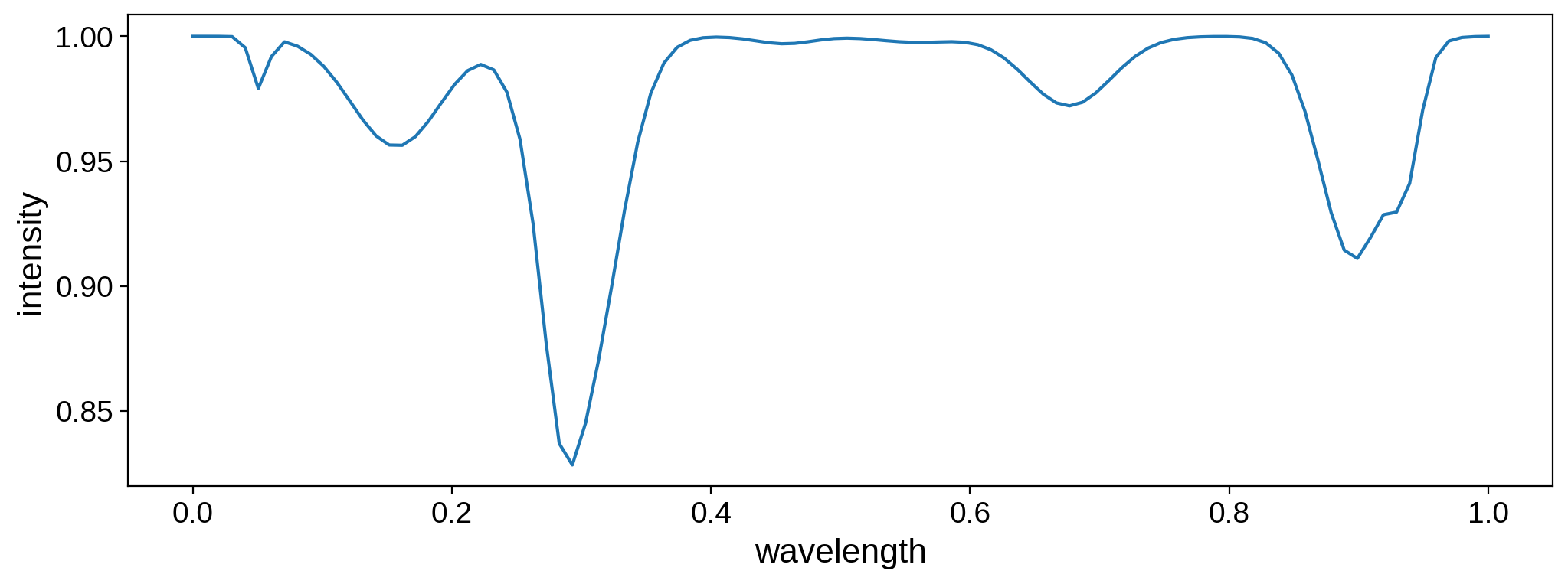
Just for fun, create a fake spectrum consisting of a few absorption lines:
The overall map amplitude¶
It’s often useful to change the overal amplitude (or luminosity) of the map at different wavelength bins. Let’s say, for instance, that we have a star with the following spectrum:
[13]:
wav = np.linspace(0, 1, 100)
amp = np.ones(100)
np.random.seed(3)
for k in range(10):
sigma = 0.05 * np.random.random()
A = 0.1 * np.random.random()
mu = np.random.random()
amp -= A * np.exp(-0.5 * (wav - mu) ** 2 / sigma ** 2)
fig, ax = plt.subplots(1, figsize=(12, 4))
ax.plot(wav, amp)
ax.set_xlabel("wavelength", fontsize=16)
ax.set_ylabel("intensity", fontsize=16);
Let’s generate a wavelength-dependent map with 100 wavelength bins. We can set the overall amplitude of the map to be equal to this spectrum as follows:
[14]:
map = starry.Map(ydeg=2, nw=100)
map.amp = amp
We can visualize it by calling the show() method, which will return an animation of the map stepping through the wavelength dimension:
[15]:
map.show()
We can also plot the flux from the map in each wavelength bin. First, note the shape of the flux:
[16]:
map.flux().shape
[16]:
(1, 100)
That’s number of light curve points versus number of wavelength bins. Let’s plot the total flux as a function of the wavelength:
[17]:
fig, ax = plt.subplots(1, figsize=(12, 4))
ax.plot(wav, map.flux().reshape(-1))
ax.set_xlabel("wavelength", fontsize=16)
ax.set_ylabel("flux", fontsize=16);
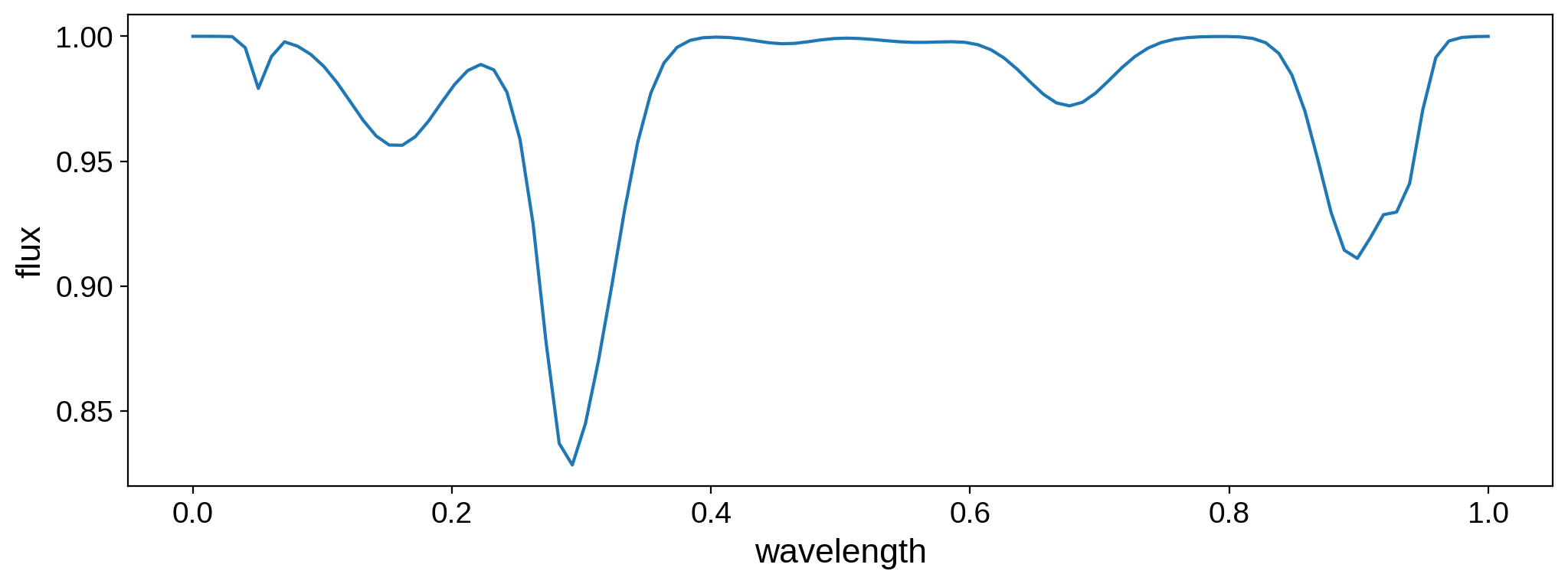
That’s our spectrum, as expected.
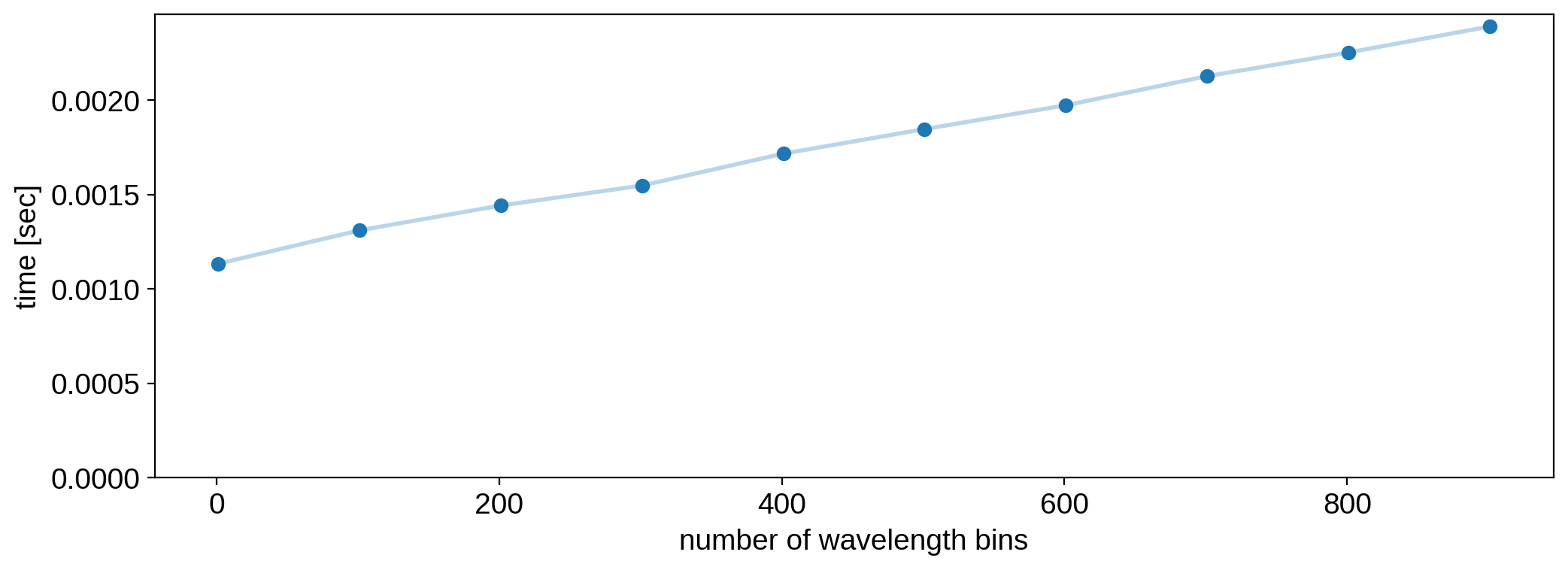
Scaling¶
Wavelength-dependent maps scale really well with the number of wavelength bins. Here’s the evaluation time for an occultation light curve as a function of the number of wavelength bins: