Note
This tutorial was generated from a Jupyter notebook that can be downloaded here.
Exposure time integration¶
Here we’ll briefly discuss how to account for finite exposure time integration, which tends to smooth out occultation light curves. Unfortunately, there’s no analytic way (that I know of) to tackle this, so the thing to do is to oversample the light curve on a fine time grid and numerically integrate over the exposure window.
[3]:
import numpy as np
import starry
starry.config.lazy = False
starry.config.quiet = True
Creating a star-planet system¶
Let’s instantiate a simple Primary object:
[4]:
star = starry.Primary(starry.Map(ydeg=0, udeg=2, amp=1.0), m=1.0, r=1.0)
And let’s give it some limb darkening:
[5]:
star.map[1] = 0.40
star.map[2] = 0.26
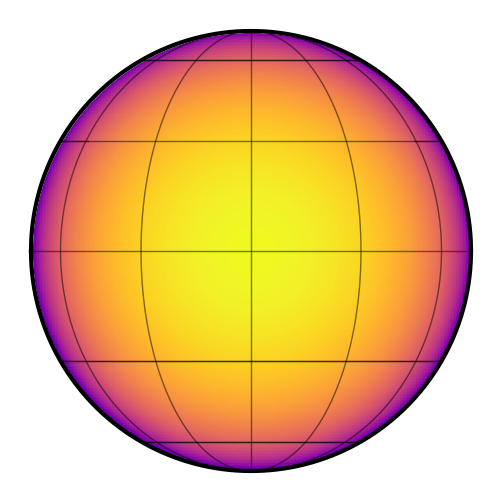
Here’s what that looks like:
[6]:
star.map.show()
Let’s now create a featureless hot Jupiter:
[7]:
planet = starry.kepler.Secondary(
starry.Map(2, amp=0), m=0, r=0.1, porb=1.0, ecc=0.3, w=30, t0=0,
)
Now that we have a star and a planet, we can instantiate the planetary system. By default, exposure time integration is disabled.
[8]:
sys = starry.System(star, planet)
Computing a transit light curve¶
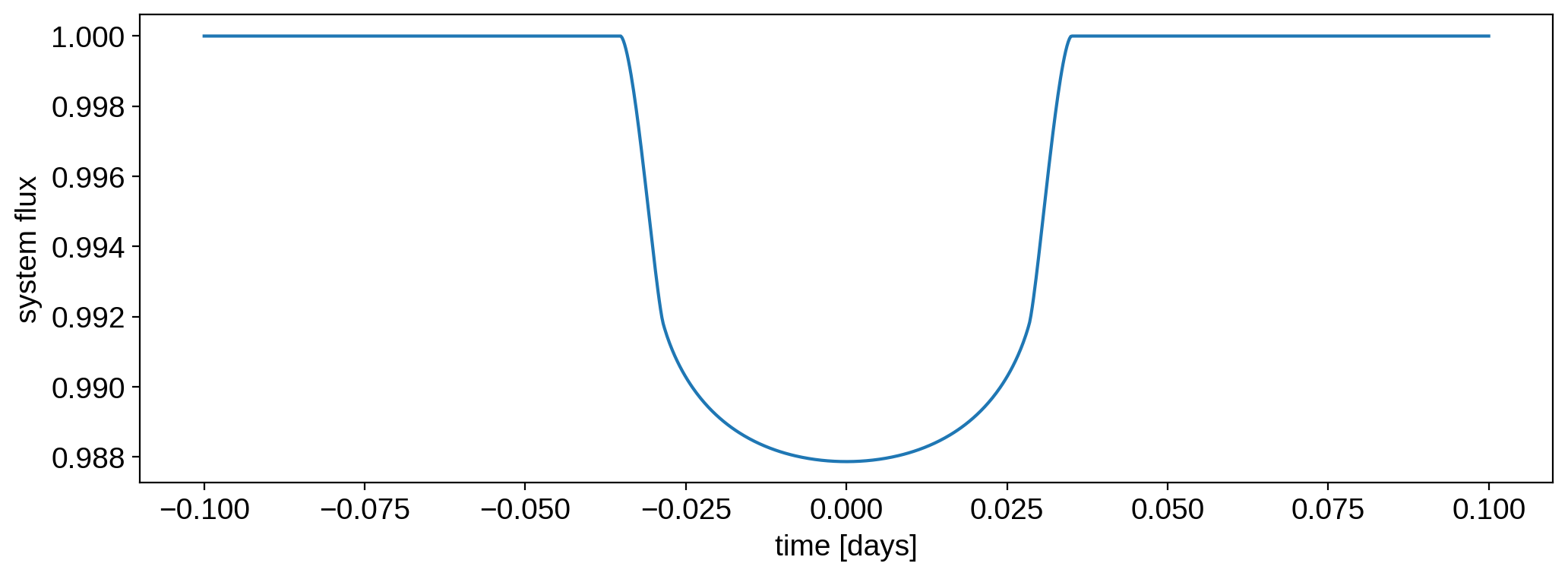
We’re ready to compute a transit light curve. Let’s do this over 1000 cadences between \(t=-0.1\) and \(t=0.1\).
[10]:
%%time
time = np.linspace(-0.1, 0.1, 1000)
flux = sys.flux(time)
CPU times: user 3.95 ms, sys: 0 ns, total: 3.95 ms
Wall time: 4 ms
Cool – starry computed 1,000 cadences in just a few ms. Let’s check it out:
[11]:
plt.plot(time, flux)
plt.xlabel("time [days]")
plt.ylabel("system flux");
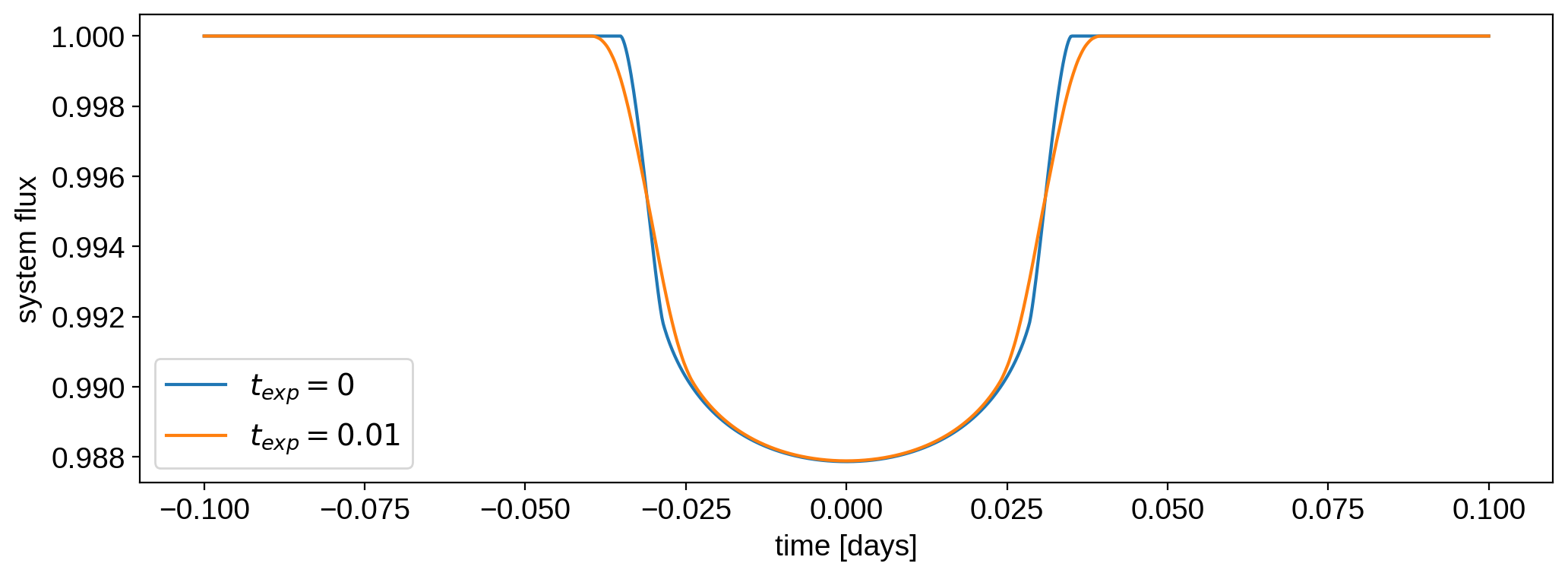
Ok, now let’s enable exposure time integration. We have to instantiate a new System object for this:
[12]:
sys_exp = starry.System(star, planet, texp=0.01, oversample=9, order=0)
We passed in the three keywords controlling exposure time integration. The first is texp, the length of the exposure window in sys_exp.time_unit (usually days). The second is oversample, the factor by which the light curve is oversampled. The larger this number, the more accurate the model will be, at the cost of extra computation time. Finally, order controls the order of the numerical integration: 0 for a centered Riemann sum (equivalent to the “resampling” procedure
suggested by Kipping 2010), 1 for the trapezoid rule, or 2 for Simpson’s rule.
Let’s compute the flux (and time the computation):
[14]:
%%time
flux_exp = sys_exp.flux(time)
CPU times: user 11.2 ms, sys: 0 ns, total: 11.2 ms
Wall time: 10.8 ms
That was a factor of a few slower than the original evaluation, but it’s not bad. Here’s the comparison of the two light curves:
[15]:
plt.plot(time, flux, label=r"$t_{exp} = 0$")
plt.plot(time, flux_exp, label=r"$t_{exp} = 0.01$")
plt.legend()
plt.xlabel("time [days]")
plt.ylabel("system flux");
Computing a phase curve¶
Exposure time integration also affects phase curves. Let’s give the planet a random map and compute its phase curve with and without exposure time integration. We’ll make the planet’s rotational period really short so we can clearly tell the difference between the two:
[16]:
planet.map.amp = 0.1
planet.prot = 0.05
planet.map[1:, :] = 0.1 * np.random.randn(planet.map.Ny - 1)
[17]:
planet.map.show()
Let’s grab just the planet flux (by passing total=False to the flux method and keeping only the second vector):
[18]:
%%time
flux = sys.flux(time, total=False)[1]
CPU times: user 4.27 ms, sys: 629 µs, total: 4.9 ms
Wall time: 2.46 ms
[19]:
%%time
flux_exp = sys_exp.flux(time, total=False)[1]
CPU times: user 14.4 ms, sys: 0 ns, total: 14.4 ms
Wall time: 7.68 ms
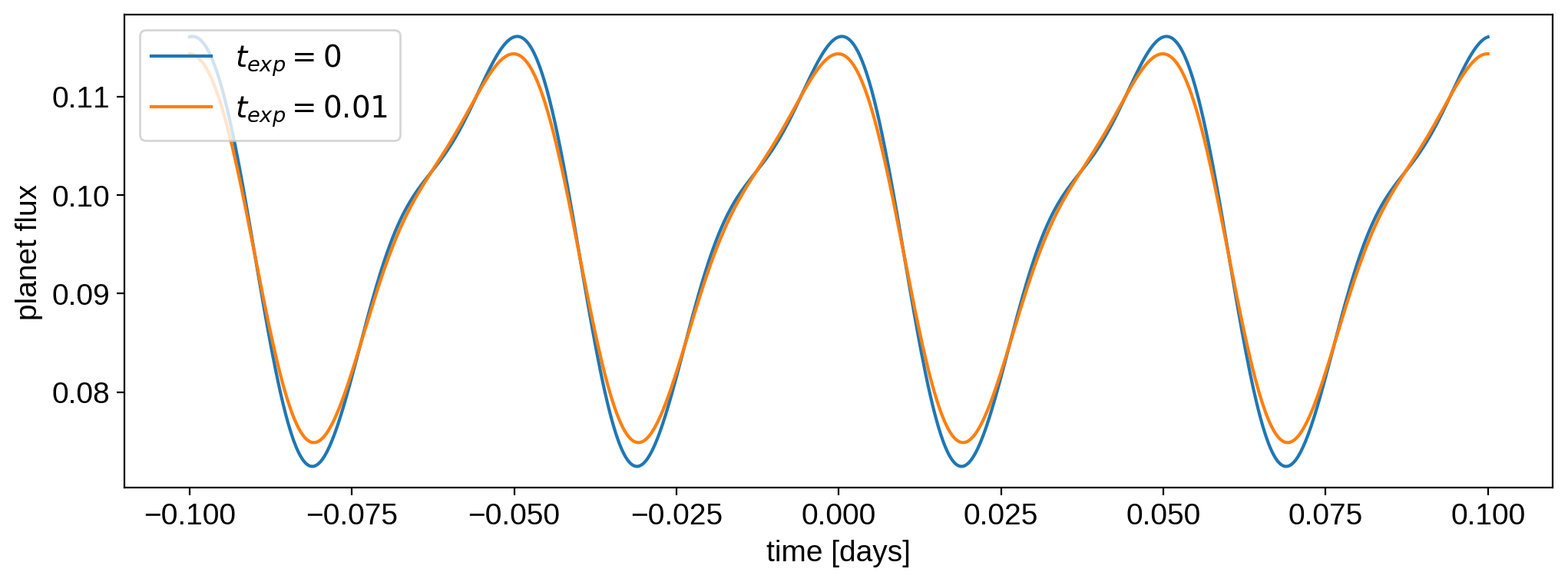
Here are the two light curves; it’s clear that the finite exposure time has smoothed out the phase curve.
[20]:
plt.plot(time, flux, label=r"$t_{exp} = 0$")
plt.plot(time, flux_exp, label=r"$t_{exp} = 0.01$")
plt.legend()
plt.xlabel("time [days]")
plt.ylabel("planet flux");